KIT-Doktorandenpreis an Dr. Ignaz Rutter
Das Karlsruhe House of Young Scientists zeichnet herausragende Dissertationen aus.
Dr. Ignaz Rutter vom Institut für Theoretische Informatik wurde im Rahmen der Akademischen Jahresfeier am 10. November 2012 mit dem KIT-Doktorandenpreis ausgezeichnet. Herr Rutter erhielt für seine an der Fakultät für Informatik abgelegte Dissertation mit dem Titel » The Many Faces of Planarity - Matching, Augmentation, and Embedding Algorithms for Planar Graphs« den diesjährigen Preis im Kompetenzbereich »Information, Kommunikation und Organisation«.
Mit dem mit je 2.000€ dotierten Preis würdigt das Karlsruhe House of Young Scientists (KHYS) herausragende Promotionen in den sechs KIT-Kompetenzbereichen. Die Auszeichnung soll den hohen Stellenwert des wissenschaftlichen Nachwuchses am KIT unterstreichen.
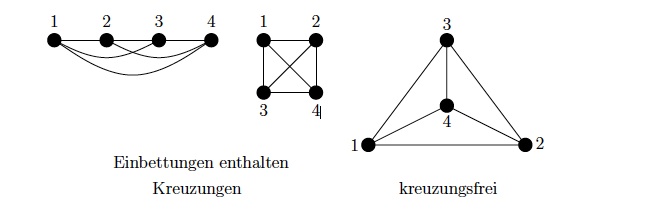 In seiner Dissertation beschäftigt sich Ignaz Rutter mit unterschiedlichen Aspekte von planaren Graphen. Ein Graph ist planar, wenn er sich kreuzungsfrei in die Ebene zeichnen lässt. Oftmals lassen sich für planare Graphen stärkere theoretische Aussagen beweisen und effizientere Algorithmen angeben als für allgemeine Graphen. Andererseits tritt Planarität oft auch als Nebenbedingung auf und macht Probleme dadurch schwieriger. Eine besondere Rolle spielen planare Graphen in der Visualisierung, da Kreuzungen die Lesbarkeit von Zeichnungen verschlechtern.
In seiner Dissertation beschäftigt sich Ignaz Rutter mit unterschiedlichen Aspekte von planaren Graphen. Ein Graph ist planar, wenn er sich kreuzungsfrei in die Ebene zeichnen lässt. Oftmals lassen sich für planare Graphen stärkere theoretische Aussagen beweisen und effizientere Algorithmen angeben als für allgemeine Graphen. Andererseits tritt Planarität oft auch als Nebenbedingung auf und macht Probleme dadurch schwieriger. Eine besondere Rolle spielen planare Graphen in der Visualisierung, da Kreuzungen die Lesbarkeit von Zeichnungen verschlechtern.
In der konkreten Anwendung ist Planarität beispielsweise beim Aufbau von Platinen von Bedeutung. Dort dürfen sich Leiterbahnen nicht überkreuzen, da sonst keine korrekte Signalübertragung mehr gegeben wäre. Außerdem ist man natürlich insbesondere daran interessiert, kompakte Layouts mit kurzer Gesamtlänge zu finden, um Materialkosten zu sparen.
In seiner Arbeit untersucht Ignaz Rutter eine Reihe von Problemen, in denen Planarität auf unterschiedliche Weise auftritt. Bei Optimierungsproblemen ist es zum Beispiel hilfreich, wenn man vorab weiß, dass das Eingabenetzwerk planar ist; in der Dissertation wird gezeigt, wie die Eigenschaft der Planarität ausgenutzt werden kann, um sogenannte Zuordnungsprobleme effizienter zu lösen. Andererseits kann Planarität Probleme auch schwieriger machen, etwa wenn man fordert, dass das Ergebnis eines Optimierungsproblems zusätzlich die Eigenschaft der Planarität erfüllen soll, da man hierdurch die Menge der möglichen Lösungen weiter einschränkt. Dies ist zum Beispiel bei Netzausbauproblemen der Fall. Das Problem ein (planares) Netzwerk durch Hinzufügen von möglichst wenigen Kanten gegen den Ausfall von einzelnen Verbindungen abzusichern ist im Allgemeinen effizient lösbar. Fordert man jedoch, dass das resultierende Netzwerk weiterhin planar bleibt, so ist dasselbe Problem NP-schwer – es ist also nicht davon auszugehen, dass ein effizienter Algorithmus existiert.
Der zweite Teil der Dissertation befasst sich mit der Visualisierung planarer Graphen, also der automatischen Erzeugung von Zeichnungen. Bisherige Verfahren zur planaren Visualisierung legen häufig zunächst die grobe Struktur der Zeichnung – die sogenannte kombinatorische Einbettung – fest und optimieren dann nur im Rahmen dieser Einbettung weitere ästhetische Kriterien, wie etwa die Anzahl der Kanten-Knicke in einer Zeichnung. Die Einschränkung auf eine einzige, anfangs gewählte Einbettung erweist sich dabei häufig als nachteilig, da sie viele Lösungen von vornherein ausschließt. Die Arbeit von Herrn Rutter stellt Verfahren vor, die es ermöglichen über alle Einbettungen eines planaren Graphen zu optimieren und unter allen Einbettungen eine zu finden, die für die Visualisierung am besten geeignet ist.
Dr. Ignaz Rutter arbeitet als Wissenschaftler am Lehrstuhl Algorithmik I von Prof. Dorothea Wagner. Er studierte Informatik an der Universität Karlsruhe und erhielt für sein Diplom den Preis als bester Absolvent der Fakultät für Informatik. Für seine Tutorien und Übungen wird er regelmäßig mit Lehrpreisen ausgezeichnet.
